Bits2Field state machine

The Bits2Field state machine is one of the auxiliary state machines used specifically for parallelizing the implementation of KECCAK-F SM. Its source code is available here.

The Bits2Field state machine ensures correct packing of $\mathtt{44}$ bits from $\mathtt{44}$ different $\mathtt{1600}$-row blocks of the Padding-KK-Bit SM into a single field element. Therefore, it operates like a (44-bits-to-1-field-element) multiplexer between the Padding-KK-Bit SM and the Keccak-F SM.

In simpler terms, it takes bits from $\mathtt{44}$ different blocks, places them into the first 44 bit-positions of a single field element, whereupon the KECCAK-F circuit runs. The name Bits2Field state machine refers to the process of taking $44$ bits from $44$ different blocks of the Padding-KK-Bit SM and inserting them into a single field element.

Although the KECCAK-F SM is a binary circuit, instead of executing on a bit-by-bit basis, it is implemented to execute KECCAK-F operations on a 44bits-by-44bits basis. This is tantamount to running $\mathtt{44}$ KECCAK-F hashing circuits in parallel.

The figure below depicts a simplified multiplexing process.

Mapping 44 Bits To A 64-bit Field Element

Suppose operations are carried out in a field $\mathbb{F}_p$ of $\mathtt{64}$-bit numbers. The smallest field used in the zkProver is the Goldilocks Field $\mathbb{F}_p$ where $p = 2^{64} - 2^{32}+1$.

After multiplexing, the 44 bits are loaded into the first 44 least significant bit-positions of the field element as depicted in the figure below.

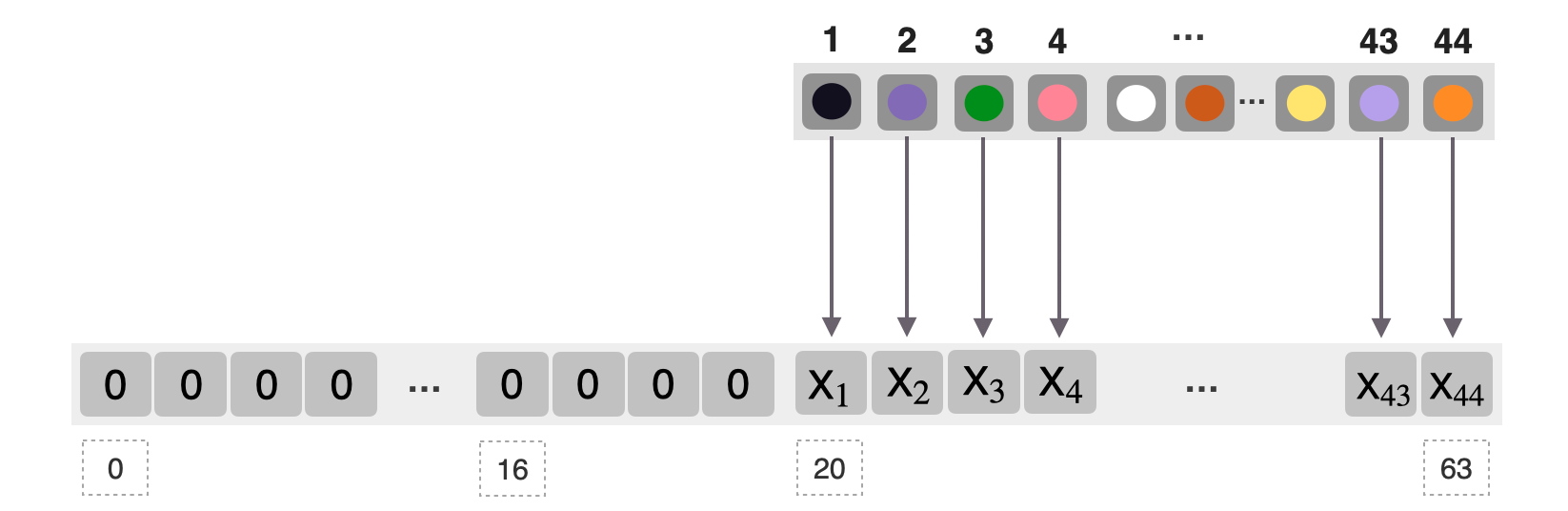
A field element as an input to the KECCAK-F circuit is of the form,

and it is composed of 20 zeroes and 44 meaningful bits related to the committed polynomials.

Given the capacity of $2^{23}$ in terms of the state machine evaluations (i.e., the degree of polynomials) and the KECCAK-F's $\texttt{SlotSize} = 155286$, one obtains $2^{23} / 155286 = 54.020375307$ KECCAK-F slots.

Therefore, a total of $54$ slots $\times$ $44$ blocks $= 2376$ Keccak blocks can be processed.

This is a big improvement from the previous $477$ blocks of the 9bits-to-1field element multiplexing (i.e., $53 \times 9 = 477$).

The Bits2Field PIL Code

The Bits2Field executor executes the multiplexing of forty-four $\mathtt{1600}$-bit blocks into $\mathtt{1600}$ field elements, where each is a $\mathtt{N}$-bit field element. For reference, see the above figure where $\mathtt{N = 64}$.

The question here is how to identify each of the original 9 bits of the field element to track their corresponding resultant $\mathtt{XOR}$ values or $\mathtt{ANDP}$ values?

Note that every bit $\mathtt{b_{i,j}}$ from the $\mathtt{i}$-th $\mathtt{1600}$-bit block is placed at the $\mathtt{2^`{i}`}$-th position of the $\mathtt{N}$-bit field element.

The PIL code therefore uses factors denoted by $\mathtt{Factor}$, such that $\mathtt{Factor \in \{ 1, 2, 4, \dots , 2^{43} \}}$, and a $\mathtt{Fieldlatch}$ after running through forty-four $\mathtt{1600}$-bit blocks.

Suppose $\mathtt{N = 64}$. Then the 44 least significant bits of the $\mathtt{64}$-bit field element looks like this:

The constraint checked is therefore,

The accumulated field element at the end of the execution (every forty-fourth row of the execution trace) is checked against the KECCAK-F input $\mathtt{KeccakF.a}$ with the boundary constraint,

The PIL code is given below.

% "bits2field.pil"

include "keccakf.pil";

namespace Bits2Field(%N);
    pol constant FieldLatch;  // [0:44,1]
    pol constant Factor;  // 1,2,4,8,...,2**43

    pol commit bit;
    pol commit field44;

    field44' = (1-FieldLatch)*field44 + bit*Factor;
    bit *(1-bit) = 0;

    FieldLatch*(field44 - KeccakF.a44) = 0;